跳跃表之初体验

一、背景

在查找算法的解决方案中，即根据 key 来查找其所在的位置，主要思想一般是基于两种，一种是基于平衡树，还有一种是基于哈希表。

而跳跃表（Skip List，下文简称跳表），也可以理解为查找算法的解决方案之一，但是它却没法归类到上述两种方案中，并且跳表实现起来也是比较简单的，在大部分应用场景下，跳表的性能是和平衡树相差无几的。

二、简介

跳跃表这种数据结构是由 William Pugh 发明的，首次公开出现于他的论文中【下载】，该种数据结构是一种很精妙的设计。

跳跃表（Skip List），顾名思义，首先它是一个 list，是一个基于链表而改进的数据结构。众所周知，链表的优势是增删，而不是查询，因为链表中每个节点都会记录并且只会记录下一个节点，所以在链表中查找数据时，是需要从首个数据开始挨个进行查找的（时间复杂度为O(n)）。而跳表的优势在于，查找数据时是不会挨个进行查找的，可以抽象理解为它是会按照某些规则跳过部分节点来进行查找的，所以查询的性能是高于链表的。

如下的简图，目标是查找77：

首先找到1，然后由于77大于1，所以找到下个等高节点20，而不是7
继续从20出发，下个等高的节点是80，所以找到80，
发现77比80小，所以继续从20出发，找下一个矮一点点的节点，此时正好找到了我们的目标值77

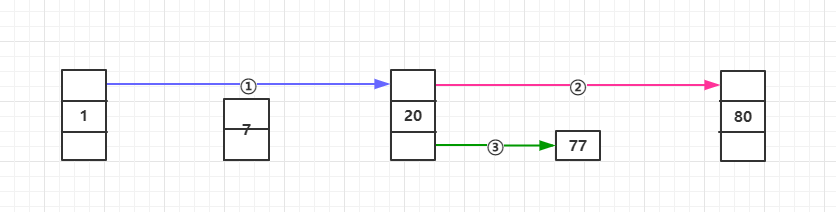
从上面的初窥中可以看出，我们要查找一个值的时候，并不需要像链表一样挨个查找，而是在期间跳过了部分节点，从而在性能上得到了提升。

另外上图中体现了一个高度的概念，如上面的第二步，我们从20开始向后查找到的节点是80而不是77，因为当时我们处于20的第三层高度，而第三层高度是指向80的，所以我们只会查找到80，但是对比发现80嫌大，所以便往下退一层，即第二层，而第二层也是指向80的，再向下到达了第一层，第一层指向的节点是77，此时正好找到了目标值。

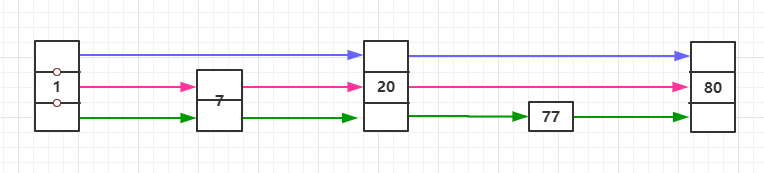
下图展示了每层的关联关系：

其实从某种意义上来说，跳表和二分查找还是有些些相似的，跳表的时间复杂度为O(log n)。

三、跳跃表中的数据插入

上文介绍了跳表的基本思路，但是是基于查询的，那么跳表是如何一步步形成的呢？换句话说，数据是如何插入的呢？

其实上文有一个概念没有讲清楚，即每个节点的层高是如何产生的，至于是如何产生的，偷偷告诉你，是在一定限制下随机生成的，哈哈哈，惊不惊喜，意不意外。

下面画图介绍了一下数据的插入过程。

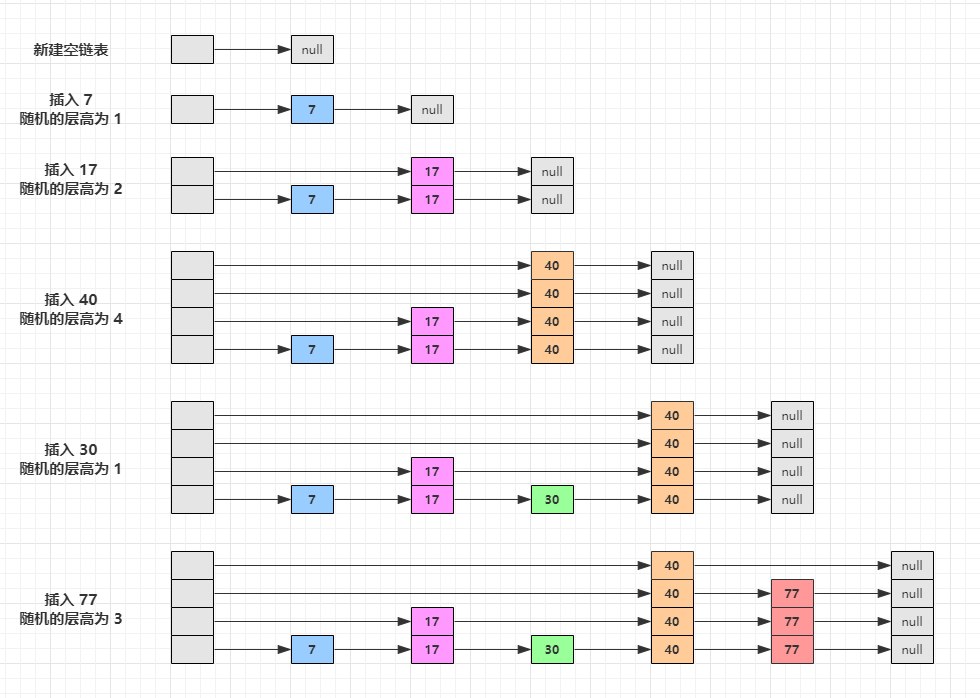
在插入一个数据的时候，会影响前后相关的关联索引，主要会影响第一层至当前层的关联索引。

在上图中，如果我们要查找30，则过程见下图中带序号的虚线：

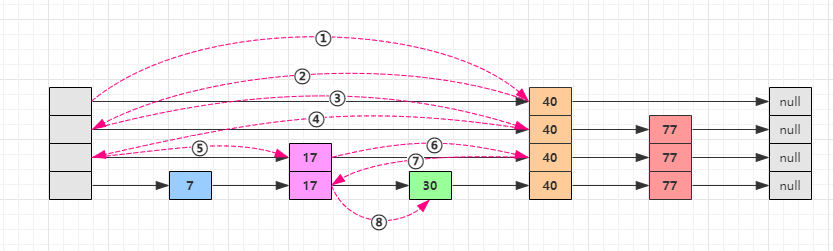
当然，在新增一个节点的时候，肯定也是要先进行一下查询动作的。

而删除节点，也是和新增的过程差不多，也是需要调整前后数据的关联索引的。

四、层数的计算

上面提到的层数是一个随机数，但是是在一定的限制范围之内的。

关于此处的限制，主要设计到两个概念:

层高上限（MaxLevel），即层高至少为1，并且不允许超出该上限，
某个有 i 层高的节点，则出现在 i+1 层的概率为 p，该 p 为固定值

在 Redis 的 SkipList 中，默认的 p 为 1/4，默认的 MaxLevel 为 32

获取层高的伪代码为：

function getRandomLevel() {
    int level = 1;
    while(random() < p && level < MaxLevel) {
        level ++;
    }
    return level;
}

至于具体的细节，建议参考 Redis 中的跳跃表，暂不赘述，此处仅用 Java 语言来大概实现一下跳跃表。

五、Java 实现

skipList

/**
* @Description: 跳跃表
* @Author: Jet.Chen
* @Date: 2019/9/16 17:39
*/
public class SkipList <T>{

    private SkipListNode<T> head,tail;
    private int nodes; // 节点总数
    private int listLevel; // 最大层数
    private Random random; // 随机数，用于投掷硬币决定是否要加层高
    private static final double PROBABILITY = 0.25; // 向上提升一个的概率（此处采用redis中的默认值）
    private static final int MAXLEVEL = 32; // 最大层高（此处采用redis中的默认值）

    public SkipList() {
        random = new Random();
        clear();
    }

    /**
    * @Description: 清空跳跃表
    * @Param: []
    * @return: void
    * @Author: Jet.Chen
    * @Date: 2019/9/16 17:41
    */
    public void clear(){
        head = new SkipListNode<T>(SkipListNode.HEAD_KEY, null);
        tail = new SkipListNode<T>(SkipListNode.TAIL_KEY, null);
        horizontalLink(head, tail);
        listLevel = 0;
        nodes = 0;
    }

    public boolean isEmpty(){
        return nodes == 0;
    }
 
    public int size() {
        return nodes;
    }

    /**
    * @Description: 找到要插入的位置前面的那个key 的最底层节点
    * @Param: [key]
    * @return: com.jet.SkipListNode<T>
    * @Author: Jet.Chen
    * @Date: 2019/9/16 17:42
    */
    private SkipListNode<T> findNode(int key){
        SkipListNode<T> p = head;
        while(true){
            while (p.right.getKey() != SkipListNode.TAIL_KEY && p.right.getKey() <= key) {
                p = p.right;
            }
            if (p.down != null) {
                p = p.down;
            } else {
                break;
            }
 
        }
        return p;
    }

    /**
    * @Description: 查找是否存在key，存在则返回该节点，否则返回null
    * @Param: [key]
    * @return: com.wailian.SkipListNode<T>
    * @Author: Jet.Chen
    * @Date: 2019/9/16 17:43
    */
    public SkipListNode<T> search(int key){
        SkipListNode<T> p = findNode(key);
        if (key == p.getKey()) {
            return p;
        } else {
            return null;
        }
    }

    /**
    * @Description: 向跳跃表中添加key-value
    * @Param: [k, v]
    * @return: void
    * @Author: Jet.Chen
    * @Date: 2019/9/16 17:43
    */
    public void put(int k,T v){
        SkipListNode<T> p = findNode(k);
        // 如果key值相同，替换原来的value即可结束
        if (k == p.getKey()) {
            p.setValue(v);
            return;
        }
        SkipListNode<T> q = new SkipListNode<>(k, v);
        backLink(p, q);
        int currentLevel = 0; // 当前所在的层级是0
        // 抛硬币
        while (random.nextDouble() < PROBABILITY && currentLevel < MAXLEVEL) {
            // 如果超出了高度，需要重新建一个顶层
            if (currentLevel >= listLevel) {
                listLevel++;
                SkipListNode<T> p1 = new SkipListNode<>(SkipListNode.HEAD_KEY, null);
                SkipListNode<T> p2 = new SkipListNode<>(SkipListNode.TAIL_KEY, null);
                horizontalLink(p1, p2);
                verticalLink(p1, head);
                verticalLink(p2, tail);
                head = p1;
                tail = p2;
            }
            // 将p移动到上一层
            while (p.up == null) {
                p = p.left;
            }
            p = p.up;
 
            SkipListNode<T> e = new SkipListNode<>(k, null); // 只保存key就ok
            backLink(p, e); // 将e插入到p的后面
            verticalLink(e, q); // 将e和q上下连接
            q = e;
            currentLevel++;
        }
        nodes++; // 层数递增
    }

    /**
    * @Description: node1后面插入node2
    * @Param: [node1, node2]
    * @return: void
    * @Author: Jet.Chen
    * @Date: 2019/9/16 17:45
    */
    private void backLink(SkipListNode<T> node1,SkipListNode<T> node2){
        node2.left = node1;
        node2.right = node1.right;
        node1.right.left = node2;
        node1.right = node2;
    }

    /**
    * @Description: 水平双向连接
    * @Param: [node1, node2]
    * @return: void
    * @Author: Jet.Chen
    * @Date: 2019/9/16 17:45
    */
    private void horizontalLink(SkipListNode<T> node1,SkipListNode<T> node2){
        node1.right = node2;
        node2.left = node1;
    }

    /**
    * @Description: 垂直双向连接
    * @Param: [node1, node2]
    * @return: void
    * @Author: Jet.Chen
    * @Date: 2019/9/16 17:45
    */
    private void verticalLink(SkipListNode<T> node1, SkipListNode<T> node2){
        node1.down = node2;
        node2.up = node1;
    }

    @Override
    public String toString() {
        if (isEmpty()) {
            return "跳跃表为空！";
        }
        StringBuilder builder = new StringBuilder();
        SkipListNode<T> p=head;
        while (p.down != null) {
            p = p.down;
        }
 
        while (p.left != null) {
            p = p.left;
        }
        if (p.right!= null) {
            p = p.right;
        }
        while (p.right != null) {
            builder.append(p).append("\n");
            p = p.right;
        }
 
        return builder.toString();
    }
 
}

skipListNode

/**
* @Description: 跳跃表的节点,包括key-value和上下左右4个指针
* @Author: Jet.Chen
* @Date: 2019/9/16 17:48
*/
public class SkipListNode <T>{
    private int key;
    private T value;
    public SkipListNode<T> up, down, left, right; // 上下左右 四个指针

    public static final int HEAD_KEY = Integer.MIN_VALUE; // 负无穷
    public static final int  TAIL_KEY = Integer.MAX_VALUE; // 正无穷

    public SkipListNode(int k, T v) {
        key = k;
        value = v;
    }
    public int getKey() {
        return key;
    }
    public void setKey(int key) {
        this.key = key;
    }
    public T getValue() {
        return value;
    }
    public void setValue(T value) {
        this.value = value;
    }
    public boolean equals(Object o) {
        if (this == o) {
            return true;
        }
        if (o == null) {
            return false;
        }
        if (!(o instanceof SkipListNode<?>)) {
            return false;
        }
        SkipListNode<T> ent;
        try {
            ent = (SkipListNode<T>) o; // 检测类型
        } catch (ClassCastException ex) {
            return false;
        }
        return (ent.getKey() == key) && (ent.getValue() == value);
    }
    @Override
    public String toString() {
        return "key-value:" + key + "-" + value;
    }
}

test

public class Main {

    public static void main(String[] args) {
        SkipList<String> list = new SkipList<>();
        System.out.println(list);
        list.put(6, "cn");
        list.put(1, "https");
        list.put(2, ":");
        list.put(3, "//");
        list.put(1, "http");
        list.put(4, "jetchen");
        list.put(5, ".");
        System.out.println(list);
        System.out.println(list.size());
    }
}

六、其它

java demo源码见地址
java 的 concurrent 包中其实也有实现，详见 ConcurrentSkipListMap 和 ConcurrentSkipListSet

本作品采用知识共享署名 4.0 国际许可协议进行许可