一、经典介绍
字符串匹配,顾名思义,就是在给定的长串字符串中,查询指定的搜索词出现的位置。身为 Java 开发人员的我接触的最原生并广泛的便是 Java 中 String 字符串中的 indexOf() 方法。
Java 中的 indexOf 方法,其算法便是使用的最易懂、最普世的 BF(Brute Force) 算法,即“暴力检索”。
实现原理见下图描述:

实现代码的话,详见 java.lang.indexOf() 方法即可。
二、KMP简介
其实,上述的 BF 算法的时间复杂度为O(mn),有很多性能更强的字符串匹配算法比其优秀,对于 Java 的优化,比如 hashmap 等数据结构在 Java8 中都得到了再次的性能提升,但是 String 中的字符串匹配却一直使用此种算法,很是好奇为什么?网上看到很多的言论,但是令人信服的有两点:其一便是“常用场景”,即字符串很多场景下的规模并不大,使用 BF 已经足够了,其二便是在其一的基础上,由于使用 BF 并不需要额外的初始化时的时间和空间开销,所以在“常用场景”之下,足矣。或许在将来的某个版本之上会有改变,但是再言之,据说其实 JVM 有内部的优化,此点暂未考量过。
所以,既然 BF 有劣势,那么就肯定有性能更好的选择,此文介绍的 KMP(Knuth-Morris-Pratt) 便是其一,其是在 BF 的基础上进行的改良。
三、实现
其实,KMP 的算法逻辑并不难理解,见下图就能够明白。
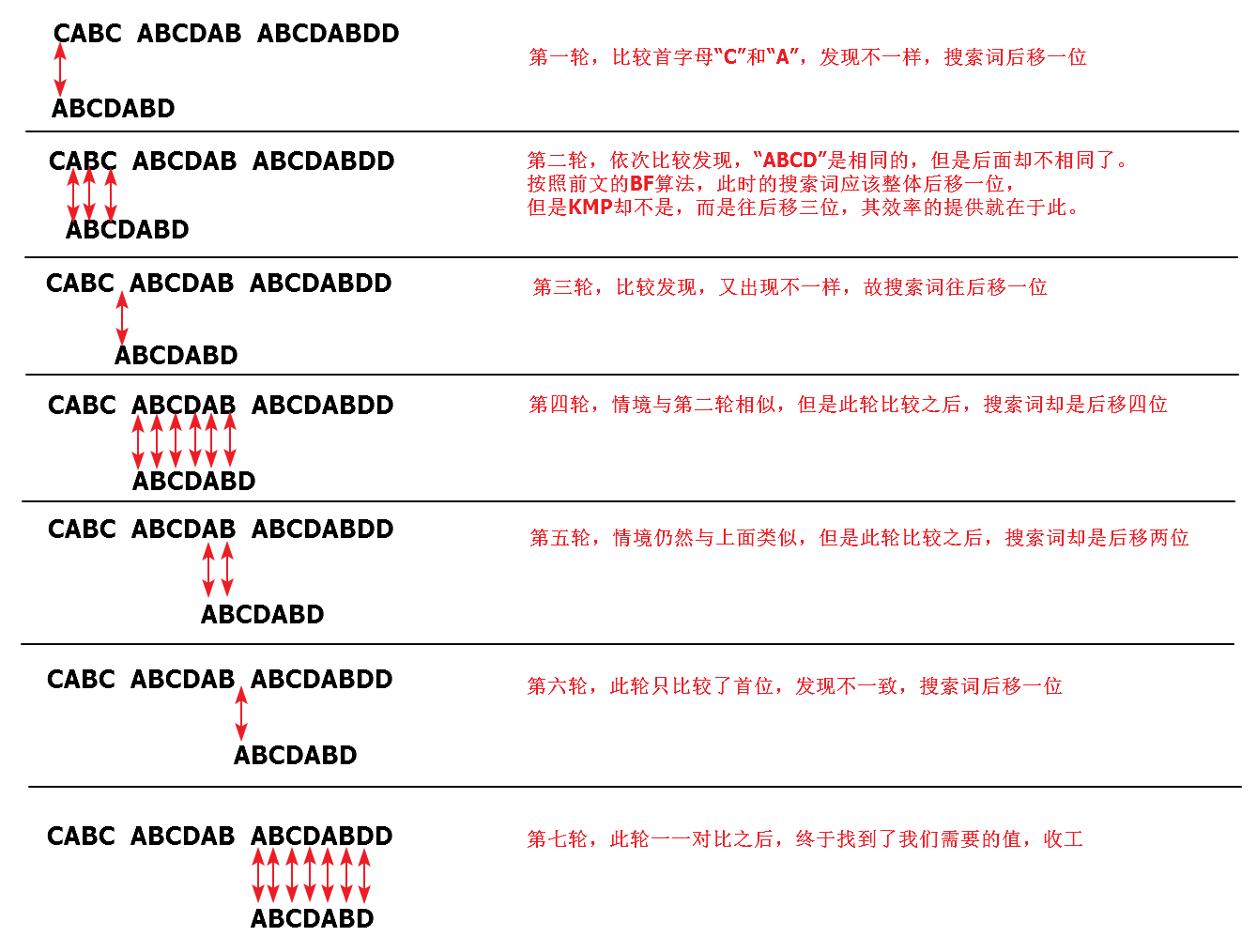
但是关键点在于,我们的搜索词到底该往后移几位呢?这里面有涉及另一样有趣的玩意儿,下面会介绍。
四、next 数组
其实,我们前文提过,为什么 Java 中的indexOf 仍采用 BF 算法的原因之一有可能是因为,在量级并不大的 String 之下使用 BF,有效地规避了时间和空间上的初始化成本,反言之,KMP 算法是需要初始化的,那么初始化成什么样?如何初始化?这里其实就是我们要讲的 next 数组,也就是上图中搜索词到底需要往后移多少位的问题的解答。
在此之前,我们先了解两个概念,“前缀”和“后缀”,前缀即除最后一位以外的其余字符组成的字符串,后缀相反。
如“ABCD”,前缀有“A”、“AB”、“ABC”,而后缀有“BCD”、“CD”、“D”。
所以,我们由前缀和后缀的概念,引申来画一张表,就是上面例子的搜索词在每位上面的前缀和后缀中重复的元素的长度,见下图:

当然,上图的“部分匹配表”,即 next 数组的计算方法只是最简单易懂的表述形式,但效率更高的计算 next 数组的算法,并不是如此简单的。
好了,第一步完成了,那么这张表该如何应用呢?
我们以上个例子中的第二轮为例,此时对比下来,有“ABC”是相同的,即第三位,查表,第三位的“C”对应的是“0”,3-0=3,所以后移三位。
再比如第四轮对比中,有“ABCDAB”是相同的,即六位数字是相同的,查表,第六位是“2”,6-2=4,所以后移四位。
总结,后移位数 = 从首开始的相同字符个数 - next数组响应的值。
五、代码实现
//KMP算法
public class KMP {
// 获取next数组的方法,根据给定的字符串求
public static int[] getNext(String sub) {
int j = 1, k = 0;
int[] next = new int[sub.length()];
next[0] = 0; // 这个是规定
next[1] = 0; // 这个也是规定
//
while (j < sub.length() - 1) {
if (sub.charAt(j) == sub.charAt(k)) {
next[j + 1] = k + 1;
j++;
k++;
} else if (k == 0) {
next[j + 1] = 0;
j++;
} else {
k = next[k];
}
}
return next;
}
// 根据给定的主串和子串,采用KMP算法来获取模式匹配
public static int kmp(String src, String sub) {
// 首先生成模式串sub的next[j]
int[] next = getNext(sub);
int i = 0, j = 0, index = -1;
while (i < src.length() && j < sub.length()) {
if (src.charAt(i) == sub.charAt(j)) {
i++;
j++;
} else if (j == 0) {
i++;
} else {
j = next[j];
}
}
// 得到开始匹配的位置索引
if (j == sub.length()) {
index = i - sub.length();
}
return index;
}
}六、总结
KMP 算法是由三位科学家的名字的首字母组成,显然该算法由他们创造。
该算法相对 BF 算法有了很大的提高,但是前提是搜索的量并不小,即如果搜索很小的字符串,那么由于初始化的原因,空间和时间的成本会增加,反而会不划算,甚至效率更低。
当然,还有更强大的字符串匹配算法,如:BM 算法等,日后再更。


文章评论